data
compression lab:
multi-resolution
source coding
related papers
basics
With advances in communications media and technologies come corresponding needs for communication techniques that take full advantage of the capabilities particular to those technologies. A prime example of such an area of growth is the medium of internet communications. With the growth of internet communications comes an increased need for techniques whereby a single user can simultaneously communicate the same information to a wide array of other users with vastly varying bandwidth resources, computational capabilities, and performance requirements. Along with a variety of other factors, this need has helped inspire a surge in interest in multi-resolution or progressive transmission source coding.
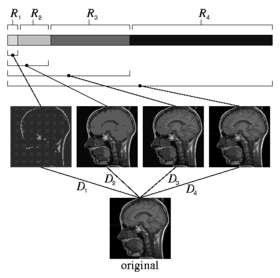
Multi-resolution source codes are data compression algorithms in which simple, low-rate source descriptions are embedded in more complex, high-rate descriptions. Use of multi-resolution source codes allows users with severe bandwidth constraints or low performance requirements to achieve a low quality data representation by only incorporating a fraction of the original coded bit stream. Users with greater capabilities or needs can achieve more precise data representations by using larger fractions of the same bit stream. Further, users uncertain of their precision needs can progressively reconstruct the data to higher and higher accuracy -- stopping the communication process when the desired accuracy is achieved. Such coding techniques are extremely valuable in any application where multiple source descriptions at varying levels of precision are required.
theory
The distortion-rate bound D(R) describes the lowest expected distortion achievable at expected rate R on a known source. Thus D(0.5) is the lowest distortion achievable at rate 0.5 bits per symbol and D(1.5) is the lowest distortion achievable at rate 1.5 bits per symbol in the above graph. The distortion-rate bound does not, however describe the optimal achievable performance for an L-resolution code with L > 1. For example, the distortion-rate function does not describe the lowest distortion achievable by adding 1 bit per symbol to a code achieving point (0.5, D(0.5)) in the above graph. Similarly, the distortion-rate function does not describe the lowest distortion achievable by reading only the first 0.5 bits per symbol from a code achieving point (1.5, D(1.5)) in the above graph. Further, the distortion-rate function does not describe all possible values of distortions D1 and D2 such that points (0.5,D1) and (1.5,D2) are achievable by the first- and second-resolution descriptions of a single two-resolution code. Theoretical work in the area of multi-resolution coding has focused on finding the space of rate and distortion vectors that can be achieved by a single multi-resolution code. The main contribution of this work was to derive equations describing the optimal performance theoretically achievable by fixed-rate multi-resolution source codes and the optimal performance theoretically achievable for variable-rate multi-resolution source codes for both stationary ergodic sources and for stationary nonergodic sources on complete separable metric spaces (which essentially describes all of the sources encountered in practical applications).
vector quantizers
Multi-resolution vector quantization is optimal multi-resolution source coding. In this case, the encoder blocks an incoming data stream into contiguous blocks of dimension n and chooses for each n-block a collection of n-dimensional reproductions. In particular, in an L-resolution code, the encoder chooses for each data block L reproductions of increasing resolution. The encoder describes the chosen collection of reproductions using a fixed- or variable-rate binary string such that the first portion of the binary string describes the resolution-1 reproduction, the second portion of the binary string describes the resolution-2 reproduction given the resolution-1 reproduction already described, and so on. The decoder decodes the desired portion of the binary string, updating its source reproduction as the binary descriptions for higher and higher resolution reconstructions become available.
wavelet-based codes
While multi-resolution vector quantizers are asymptotically optimal source codes -- that is they achieve performance arbitrarily close to theoretical limit as the dimension approaches infinity -- for practicality reasons, multi-resolution vector quantizers are typically implemented at very low vector dimensions. Giving up optimal encoders and decoders for ones that are merely good (and clever!) yields much of the high-dimension advantage without the computation, memory, and delay costs associated with high dimensional codes. Wavelets are an especially useful technique for achieving much of the high-dimensional advantage at very low complexity, and are therefore extremely popular in modern multi-resolution data compression algorithms. Ongoing work aims to combine the results of multi-resolution source coding theory with the techniques used in practical multi-resolution data compression algorithms like SPIHT, EZW, and their descendants.